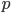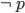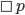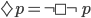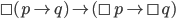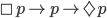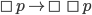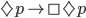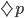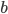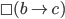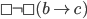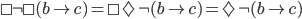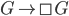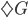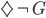So g and I were discussing the nature of Consciousness in another thread, and he said something here that I've been meaning to reply to for a while. We were discussing Chalmers' arguments (described in this paper and elsewhere) that Consciousness cannot be deduced from the Laws of Physics.
g wrote in part:
Consciousness-mysterians have in effect adopted a strategy that guarantees that their questions cannot be answered. There simply isn't any evidence one could possibly present, any argument one could possibly make, that would count as showing that consciousness is a physical phenomenon. [This] is the key difference that Chalmers points out, though of course he does so in terms more sympathetic than mine to consciousness-mysterianism. And it's also what you draw attention to, again with a spin different from mine :-).
But, really, doesn't making that argument trigger at least a feeling of unease? What you're saying comes down to this: nonphysicalism about consciousness is unfalsifiable even in principle: no possible evidence could ever suffice. Usually unfalsifiability is a serious problem for a theory. Personally, I'm only comfortable holding an uncheckable-even-in-principle belief with much confidence if (1) I think I can actually prove it from first principles (note: observing that it's unfalsifiable doesn't count!) as with pure mathematics or statements that are true by definition, or (2) I can't avoid holding it because it's an unavoidable load-bearing element of my cognitive apparatus, as with those first principles themselves. In Bayesian terms, an uncheckable belief can't accumulate evidence, so it has to come from your prior, and I prefer my priors without too much unnecessary stuff built into them :-). And nonphysicalism about consciousness seems to me very much not the sort of thing covered by either #1 or #2. -- Of course, your attitude to unfalsifiability need not be the same as mine.
Yeah, as you guessed, I don't think this is a proper use of the criterion of falsifiability. Let me try to explain why I think this.
In what follows, I will be assuming that my audience is familiar with some basic philosophy lingo, as well as the first Chalmers essay I linked to.
Also, please note that I am only a "nonphysicalis[t] about consciousness" in a very specific sense which will hopefully become clear in what follows. (I'm okay with somebody who wants to say that the mind and brain are in some sense identical, as long as they don't claim to be able to prove this identity from the laws of physics.)
I. Goodbye, Eliminativism
Before I begin, I want to clear one bugbear out of the way; readers who wish to cut to the chase might want to skip this section. Some philosophers of mind are eliminative materialists, they think that Consciousness isn't really even a thing that exists, and that the concept should be completely removed from a truly scientific account of the world. (This position is very different from the reductionist position the rest of my essay will be discussing, where you say that Consciousness does exist but that it can be derived from more fundamental concepts.)
I'm not sure that Eliminativism even deserves to be given the time of day, since to me it is just obvious that conscious and perceptual experience is a thing. <checks mind> Yup, I have experiences! Furthermore as many people have noted, it is impossible to even argue for eliminativism without using language which presupposes the existence of mind and beliefs (e.g. "I think Eliminativism is true", "I believe the hypothesis for this reason", "it is justified by our knowledge of these observations in the laboratory", "appearances are an illusion; they merely appear to exist", "no rational and scientifically-minded person could avoid realizing that..." etc. etc.) A consistent eliminativist would have to give up all the terms in red, and that would make them unable to express any theories at all.
If that were not enough, anyone who wants to talk about falsifiability (or any other version of empiricism) had better keep the idea of Consciousness around. For the core of that idea, is that a good scientific theory ought to make at least some predictions about things we actually experience so that they can be ruled out by the data if they are wrong. The technique of observation—which is conscious by definition—is implicit in the scientific method. What is the point of even doing an experiment in the laboratory, with some elaborate but mindless machine if, at the end of the day, no human being checks to see what the results of the experiment are?
Experience is bedrock; that is what we use to test the existence of other, unobserved things! If you doubt the existence of experiences, then you have no reason to accept the existence of anything else. So this is one of those "first principles" that g refers to in his comment.
Hence Consciousness exists. Now of course, there is one very obvious sense in which the existence of consciousness isn't falsifiable. Namely, that if there weren't any conscious beings, then you wouldn't be around to notice their absence. But, that is not the kind of falsifiability puzzle that g was talking about. He wasn't suggesting that the existence of consciousness should be falsifiable, but rather that certain kinds of theories about its true nature should be falsifiable. Let us see.
II. Why Conceptual Truths aren't Falsifiable.
If we ask a question like "Are p-zombies conceivable", then it seems to me we're basically asking a question about the structure of logically possible worlds. Is there a logically possible world in which there are entities physically like us which do not have the property of Consciousness? (In what follows I will treat "logical possibility" and "conceivability" as synonyms, although some philosophers are likely to wish to make a distinction between them.)
Now, questions about what is logically possible are not really empirical questions. Because, empiricism can only tell us which of the logically possible worlds we actually live in. It cannot tell us which worlds are possibilities in the first place. Instead, we reason about possible worlds by doing a conceptual analysis of the concepts in question. This seems like it is necessarily an a priori sort of analysis, because the space of possible worlds should not depend on which of the worlds is actually the case. And if such truths are a priori, then we shouldn't expect it to be falsifiable, we should in fact expect it to be nonfalsifiable, like the truths of mathematics.
(I've previously written a bit about Reasonable Unfalsifiable Beliefs before. I'm not sure it really gets into the issue I'm describing here, but one of the things I discussed there is how certain propositions can be unfalsifiable while still possessing significant evidence in their favor.)
Now, that doesn't mean that positions about the logical conceivability of worlds should always be held in a completely dogmatic way. It may be that in some cases, you have to do a tricky conceptual analysis of a concept (in this case "Consciousness") to determine what we in fact mean by the word, before you can decide what is or is not entailed by its existence. Nor does it mean that you should be impervious to updating your beliefs; it just means that the proper method for changing your beliefs is through philosophical discussion rather than through scientific collection of data: somebody might say something like "You think that X is impossible, but what if it happened in way Y, did you think of that?"
(And then you might say "No I didn't think of possibility Y, thanks for pointing out the flaw in my argument, I owe you big time!" or maybe "You idiot, Y isn't at all applicable to what I said because blah blah blah..." and then the conversation could continue from there...)
Thus, believing that something can be demonstrated a priori on conceptual grounds without resort to empericism, is not quite the same thing as assigning a strictly 0 prior probability to being wrong. A complicated math proof is true a priori, but there is still the possibility of having made an error somewhere in the proof. Rather, it is a statement about by what methodology one knows the truth in question.
III. Can you tell me a story?
Although empirical observation doesn't directly tell us about which worlds are logically possible, there is still a limited role that observation plays through developing the exercise of the imagination. We may become more aware of certain logical possibilities as a result of learning certain things about the world. So for example, if somebody stupidly said that it was a priori impossible for Newtonian mechanics to be wrong and then we did experiments and found it was wrong, then that might be taken to refute the position. But in this case the foolishness of the claim could have been revealed beforehand by imagining with sufficient clarity the scenario in which Newtonian mechanics is false. It needn't have actually happened that way to refute the position. (It's a bit like Nature saying, in a particularly hard-to-ignore voice, "Have you considered the possibility that Newtonian mechanics is wrong?")
What that means, is that if you think that Science will eventually show that Consciousness can be deduced from the physical facts about the brain, then in principle you ought to be able to write a science fiction story now about a set of observations, such that reasonable people would agree that if those observations came to pass, then Consciousness would be fully explained in physical terms. You see, the most magical thing about Science is its ability to check things through observation, but I am waiving that requirement here by allowing you to make up whatever set of observations you like. And that makes it harder to say "Science will one day show...", since if you can't write the science fiction story you can't plead lack of funding or experiments. You can only plead lack of imagination.
(In this very, very limited sense, the position that Consciousness can't be reduced to the Laws of Physics can be falsified. It would be falsified if we found some scientific facts that made reasonable people spot the error in the philosophical arguments of people like Chalmers. But then again it would also be falsified if you can even write a science fiction story that points out the errors in Chalmers' arguments! On the other hand, once one is willing to accept the possibility that Science could refute seeming conceptual truths, then the belief that Science can explain Consciousness now becomes the unfalsifiable belief, because even in the face of a complete failure to imagine what an explanation would look like, one could always hope that a future scientific revolution will change everything!)
One test of a priori knowledge is that we cannot even conceive of a scenario in which something isn't true. (For example, I can't conceive of a scenario in which 2+2=5.) If that is really true, then it actually implies that the position isn't falsifiable. But that shouldn't make us uncomfortable unless it's the kind of proposition we wouldn't have expected to be a priori.
(Of course you can always imagine an idiotic position which can't be falsified because the person who holds it insists on holding it no matter what and keeps modifying the hypothesis to save it. For example, someone (it is just barely possible) might believe in Young Earth Creationism no matter what the experiments of Biology, Geology, and Physics find, because they think that this is merely God testing them or whatever. But that is not really so much because YEC is unfalsifiable, it's more because the person refuses to recognize that their position is falsified even when the facts do falsify it. It's a very different case if you can't think of any facts which would convince a reasonable person that the belief is wrong.)
IV. A Primer on Modal Logic
When it comes to the Philosophy of Mind, many of these disputed propositions are explicitly about what is logically possible (or conceivable). In particular, I think the dispute between Chalmers and more reductionistic philosophers—for example Daniel Dennett—is like this.
If Chalmers is right about Consciousness, then he has to be right a priori. But the same goes for Dennett—if he's right that Consciousness can in principle be reduced to physical statements about the brain, then I think his position that this is conceivable would also have to be right a priori. [1] As I have been saying, any true statement about which things are logically possible, must itself be logically necessary: if true, necessarily true; if false, necessarily false. Thus, whoever is correct, we can't really expect that their position will be empirically falsifiable.
We can formalize the arguments I've been making a little bit using Modal Logic. In this system of notation, if 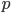 represents that a proposition is true, and
represents that a proposition is true, and 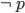 (i.e. not p) that it is false, then
(i.e. not p) that it is false, then
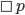
is the statement that
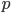
is a
necessary truth, while
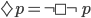
is the statement that
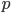
is a
possible truth. One then assumes certain reasonable seeming axioms, including (N) that the theorems of Modal Logic are necessary truths and (K) that
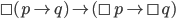
. People also usually stipulate that
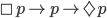
, since necessity implies actuality, while actuality implies possibility.
There are actually multiple possible interpretations of exactly what we mean by necessary and possible, but the one I currently have in mind is the notion of analytic possibility, where 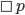 means that
means that 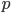 follows from pure logic, together with the conceptual meanings of whatever words enter into the proposition
follows from pure logic, together with the conceptual meanings of whatever words enter into the proposition 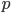 .
.
Under this particular interpretation, it seems unreasonable not to accept the following axioms of modal logic:
(S4) 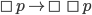
(S5) 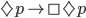
These axioms formalize the idea, which I've defended above, that logic is true for a priori conceptual reasons, so that the same rules of logic are valid in all logically possible worlds.
(Of course in normal life we often talk about necessity in a much looser way, e.g. you can say that if Joe is a bachelor it is logically impossible (hence necessarily false) for him to have a wife, but since he could have gotten married to Sally 5 years ago, it wasn't necessarily impossible for him to be married. This forms a seeming counterexample to S4 but this is only because the scope of the necessities are different. If  always means absolute logical necessity, taking into account all possible variations, then such counterexamples do not arise.)
always means absolute logical necessity, taking into account all possible variations, then such counterexamples do not arise.)
The axioms (S4) and (S5) have an interesting consequence. Any time a proposition has multiple modal symbols in front of it, for example  , this assertion is always equivalent to to removing all but the last modal operator. So this complicated proposition is equivalent to simply
, this assertion is always equivalent to to removing all but the last modal operator. So this complicated proposition is equivalent to simply 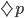 . This fact will be useful in the next section.
. This fact will be useful in the next section.
V. The Burden of Proof
Since both philosophers are making a priori claims, we have to be very careful about determining which of them has the "burden of proof".
Usually I find it annoying and unproductive when philosophical arguments degenerate into discussions of who has the burden of proof. Nevertheless, it's fairly reasonable to take claims that something is logically necessary (or logically impossible) to have a very high burden of proof; if there isn't a good reason to believe it, then we disbelieve it. It is an unreasonably strong claim to say that logic proves that pigs cannot fly. Even though in the real world, they usually tend not to. (But there are always exceptions. When we were flying my cat to the East Coast, my Grandpa took the opportunity to ask the animal handler there. It turns out that pigs do fly, at least on United Arlines.)
Conversely, claims of logical possibility have a low burden of proof; if we don't know of any proof that something is impossible, then it is probably possible. (And if we know there can't be a proof that something is logically impossible, then presumably it must be logically possible, since logical possibility just is that which does not lead to any logical inconsistency. [2])
But in this case both philosophers' views can be phrased as making strong claims of logical necessity! To paraphrase:
Team Chalmers: It is conceptually impossible (i.e. necessarily false) for Consciousness to be fully explained in strictly physical terms.
Team Dennett: It is conceptually impossible (i.e. necessarily false) for p-zombies to exist (at least, given sufficient information about the workings of the brain).
So here we have two conflicting philosophical positions, and both sides are staring at the other, thinking that the other team is making an absurdly overconfident claim. So who is really being cocky here?
I think we can resolve this issue by using modal logic. What Team Dennett is really committed to is this proposition:
Strong Physicalism: Given the Laws of Physics (taking the usual form of mathematical field equations), one can logically deduce that certain physical systems such as the brain (assuming they exist) possess the property of Consciousness.
While it is an empirical physics question what the exact Laws of Nature are, and an empirical biology question how exactly our brain is wired, these empirical propositions are not really the essential part of the hypothesis in question. It seems unlikely that the dispute between Chalmers and Dennett really comes down to the exact equations of the Standard Model, or the exact way in which the neurons are connected. Let us suppose hypothetically that all of these scientific details are known, the interesting question is whether assuming all that, Consciousness follows by purely logical considerations.
I have called this position Strong Physicalism, because one could imagine a Weak Physicalist position which states that Consciousness follows by some weaker mode of necessity, for example metaphysical necessity (that which is necessary in itself, given the fundamental nature of things, even if human beings are not capable of proving it), or perhaps necessary given certain additional principles, that might be plausible to postulate. [3]
Now the thing to notice is that Strong Physicalism itself contains a logical modal operator  within it. If we let
within it. If we let 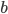 be a list of physical facts about a human brain (which are of course logically contingent, since human beings do not exist by logical necessity), and we let
be a list of physical facts about a human brain (which are of course logically contingent, since human beings do not exist by logical necessity), and we let  be the proposition that this human being is conscious, then we can restate each team's claim of logical necessity as follows:
be the proposition that this human being is conscious, then we can restate each team's claim of logical necessity as follows:
Team Dennett: 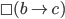 (from Strong Physicalism)
(from Strong Physicalism)
Team Chalmers: 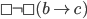 (Strong Physicalism is necessarily false)
(Strong Physicalism is necessarily false)
But by the rules of modal logic, 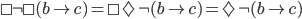 , a mere possibility claim.
, a mere possibility claim.
So this makes it clear. Team Dennett is making the claim that a first-order proposition, one that does not involve any modal symbols, is necessarily true. This is a very strong claim and the burden of proof is on them to show it.
On the other hand, Team Chalmers is making a claim that a second-order proposition, one that involves a modal symbol, is a necessary truth. But all second-order propositions about logic partake of necessity; either they are necessarily true or necessarily false. Hence, this is an exception to the usual rule that claims of a priori necessity have a strong burden of proof.
Instead, one should strip off all but the last modal symbol. When one does this, one can see that Team Chalmers is actually making a possibility claim about the first-order propositions. Hence their claim is almost certainly true, unless there is good reason to think that Team Dennett's beliefs might follow from the structure of logic itself. If there is a good argument for that, I am still waiting to hear it. (Arguments about how amazing the progress of Science has been to date, of course do not qualify as arguments about the structure of logic!)
It was this realization, back when I was a grad student, that put me firmly in Chalmers' camp.
One might worry that this is a bit of a trick and that I could have rephrased things in a way where the argument could be run in reverse, so that by rearanging the terms somehow it would appear that the Chalmerites were making the 1st order necessity claim and the Dennettites the 2nd order necessity claim. [4] But I don't see any way of making that permutation convincingly. Strong Physicalism is (as it says on the tin) a very strong claim, which has a  in it by its very definition. Nobody is forcing anyone to go around making super-strong claims of logical necessity. Strong theses have powerful implications, but for that very reason they are very easy to refute.
in it by its very definition. Nobody is forcing anyone to go around making super-strong claims of logical necessity. Strong theses have powerful implications, but for that very reason they are very easy to refute.
As I have said all along, there are weaker versions of physicalism which don't make such strong claims, and I'm not saying that those views can be ruled out so easily. But these are precisely the versions of physicalism which do preserve some degree of mystery when it comes to Consciousness. [3 again]
VI. Occam's Shaving Cut
A scientifically-minded person might be tempted to retort, "Well hang it all, you're missing the entire point here! Forget your sophistical modal argumentation, isn't it so much simpler to just assume that consciousness is physical, not some weird additional new thing? Occam's Razor, which as you well know is a foundational principle of science, states that we should usually go with the simpler view until the data makes it untenable. And postulating some crazy new mysterious stuff besides the laws of nature (that work so well in other areas) is anything but simple."
But I think this is a misapplication of the Razor, likely to lead to shaving cuts. The normal use of Occam's Razor is when we have two or more logically possible hypotheses, each of which is compatible with the data, and we want to figure out which of them is most likely to be true. In Bayesian terms, the simpler hypothesis is often (though not always) the one with the higher prior probability.
But Strong Physicalism isn't a hypothesis about which of the logical possibilities corresponds to the real world. It's a hypothesis about the space of logical possibilities itself! It is a category error to say that the space of logical hypotheses must itself be simple, since it simply consists of all thinkable hypotheses (however complicated or absurd). Do you think would be absurd for p-zombies to actually exist? Good! I do too! But that doesn't mean it doesn't exist as a logical possibility. There is no limit to how complicated or absurd a logical possibility can be, as long as it is not self-contradictory.
When we use Occam's Razor, we are generally presupposing that we have already successfully identified the space of logical possibilities, and that we have already used ordinary logic to figure out what each hypothesis says. We can use the Razor to say "Hypothesis X is better because it is simpler and still logically implies observation Y". But we shouldn't use it to say "It is better to think that X logically implies Y (even if I can't see how it does), because things would be so much simpler if it did imply Y than if it didn't!" Whether or not X explains Y is a feature of the logical structure of X and Y, and that is not the sort of thing we ought to be applying Occam's Razor to.
Now I admit that if X is a very successful theory, and there is genuine reason to think it might imply Y if we just did some very complicated calculation properly, then of course we should probably give X the benefit of the doubt instead of assuming we need to find a better theory. This happens all the time in Physics. But even in these cases, whether or not X implies Y is still a fact about pure logic. It either does or it doesn't follow. If it turns out that X doesn't imply Y, then no amount of wishful thinking about simplicity can make it oblige. Logical consistency trumps Occam's Razor, every time.
This is why mathematicians don't use Occam's Razor all that often. I won't say there is no use for it; sometimes one can detect patterns in numbers empirically, and it may be reasonable to guess that the patterns continue in the simplest way. But mathematicians aren't satisfied with that, because in their domain you can usually prove logically what is or is not the case, which is a much better method.
And the issues raised by Chalmers and Co. aren't really a matter of complicated calculations—they aren't saying, "oh but Consciousness is so complicated, so how can it arise from a simple thing like the brain?" That would be ridiculous, since as we all know the brain is fiendishly complicated. (I feel like I really ought to link to some amazing pop-sci article about neuroscience here, but I'm having difficulty finding the right one. Maybe an Oliver Sacks book?) Rather they are pointing out a logical gap that seems to exist no matter what we postulate about the workings of the brain.
The way to bridge that gap would be to write a description of a physical system that just is logically identical to that system having experience and awareness. One could propose definitions like "processes information in such and such complicated way blah blah" but then one still needs to show that this is identical to our subjective feeling of awareness, which most certainly exists (see section I). And I don't see how this could possibly be done, without postulating some additional bridging principles.
VII. Thanksgiving
Since today is Thanksgiving Day, it seems appropriate to end by expressing my gratitude that Consciousness is real. Since without it, we would be unable to appreciate any of our other blessings!
Footnotes
Footnote 1: Somebody might propose that Consciousness could arise in two different logically possible ways, and that one way is reducible to physics, while the other way is not. Then it could be a empirical question which of these two categories human Consciousness happens to fall into in the real world. For purposes of my argument, I am treating such a scenario as a special case of Dennett's viewpoint, because (as I think Chalmers would admit) if it is conceivable for Consciousness to be reduced to purely physical properties about a sufficiently complex physical system, there is no particularly good reason to believe that the brain couldn't be an example of such a complex system.
Footnote 2: Some caveats may be in order here about Gödel's incompleteness theorems, and "ω-inconsistency". To be brief, in some cases the shortest "proof" that a statement is logically inconsistent might be infinitely long; in which case such infinite proofs must be included for my statement in the main text to be true. However, I very much doubt that this subtlety of mathematical logic is particularly relevant to the subject of Consciousness, since the brain is a finite system and so it seems that any relevant proofs ought to be completable in a finite number of steps.
(Some people have proposed a different role for Gödel's theorem, claiming that the ability of human beings to reason about math proves that our intellectual capacities cannot be reduced to computation. But I think these arguments are bunk! First note that Gödel's theorem only states that a formal system for proving mathematical truths by rote cannot be both complete and consistent. Whereas human beings reason primarily by informal methods, so Gödel's theorem does not seem to apply to us in any obvious way. So this does not prove intellect cannot be reduced to computation, because (a) there is no reason to think that human beings are capable of proving all true arithmetic propositions, and (b) there is no reason to think an intelligent AI couldn't reason about mathematics in an informal way, and if it were truly intelligent, it probably would!)
Footnote 3: Note that in Chalmers' classification, "Type B" materialism (which asserts that the brain and mind are ontologically identical, but that we can only grasp this identity as an a posteriori truth) is actually an example of Weak Physicalism. For this reason, I don't think it is ruled out by any of the arguments I've made here. This view is oddly similar to the Chalcedonian explanation of how Christ can be simultaneously divine and human.
Footnote 4: An example of a modal argument which can be run in reverse is the question-begging Modal Ontological Argument for the existence of God. There you assume 1. if God exists, he does so necessarily: 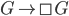 , and also 2. the existence of God is at least possible:
, and also 2. the existence of God is at least possible: 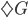 , and from there you can turn the crank of modal logic to prove 3. that Theism is a necessary truth:
, and from there you can turn the crank of modal logic to prove 3. that Theism is a necessary truth:  . But if you had instead assumed that Atheism is at least possible: 2'.
. But if you had instead assumed that Atheism is at least possible: 2'. 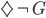 , then you can instead prove that God is impossible: 3'.
, then you can instead prove that God is impossible: 3'.  . While either argument is technically logically valid according to the rules of modal logic, a fallacy comes when you try to get people to interpret
. While either argument is technically logically valid according to the rules of modal logic, a fallacy comes when you try to get people to interpret 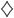 in the 2nd premise in a weak epistemic sense, saying they should accept it because it at least theism seems not to be logically self-contradictory, whereas the first premise is only plausible as a claim about metaphysical necessity, not a claim about logical necessity.
in the 2nd premise in a weak epistemic sense, saying they should accept it because it at least theism seems not to be logically self-contradictory, whereas the first premise is only plausible as a claim about metaphysical necessity, not a claim about logical necessity.